Welcome to Lesson 19 Problem Set 7.1! In this problem set, we embark on an exciting journey into the realm of mathematics, exploring fundamental concepts and methods that will equip you with the tools to tackle complex problems with confidence.
Through a series of carefully crafted problems, we will delve into the intricacies of mathematical thinking, developing a deep understanding of key principles and their practical applications in real-world scenarios.
Definition and Purpose of Lesson 19 Problem Set 7.1
Lesson 19 Problem Set 7.1 serves as a pivotal component in the curriculum, reinforcing the foundational concepts and skills introduced throughout the preceding lessons.
This problem set specifically focuses on honing students’ abilities in solving equations and inequalities involving absolute values, a crucial topic in algebra that forms the basis for more advanced mathematical applications.
Key Concepts and Methods: Lesson 19 Problem Set 7.1
This problem set delves into fundamental mathematical concepts and methods that are essential for understanding and solving problems related to limits and continuity.
One of the key concepts is the epsilon-delta definition of a limit, which provides a precise mathematical framework for determining whether a function approaches a specific value as the input approaches a specific point.
Epsilon-Delta Definition of a Limit
The epsilon-delta definition of a limit states that for a function f(x) to have a limit L as x approaches a, there must exist a positive number δ such that whenever |x – a|< δ, then |f(x) - L| < ε for any given positive number ε.
This definition allows us to prove the existence of limits rigorously and to determine the specific value that the function approaches.
Other Concepts and Methods, Lesson 19 problem set 7.1
Other important concepts and methods employed in this problem set include:
- Algebraic techniques for manipulating expressions involving limits
- The squeeze theorem, which allows us to determine the limit of a function by comparing it to two other functions with known limits
- The concept of continuity, which measures the smoothness of a function at a particular point
By applying these concepts and methods, we can effectively analyze the behavior of functions and determine their limits and continuity.
Step-by-Step Problem-Solving
To effectively solve the problems in this problem set, follow these steps:
1. Read the Problem Carefully
Start by thoroughly reading the problem statement. Identify the given information, what is being asked, and any constraints or conditions. Understanding the problem’s context is crucial.
2. Plan Your Approach
Once you understand the problem, consider different strategies to solve it. Determine the concepts and methods that apply to the problem. Sketch out a plan or Artikel of your approach.
3. Solve the Problem
Implement your plan by applying the relevant concepts and methods. Show all your work, including any equations, formulas, or calculations. Clearly explain your reasoning and thought process.
In the midst of tackling Lesson 19 Problem Set 7.1, I stumbled upon an intriguing topic: the net worth of Five Marys Farm. I couldn’t resist clicking on this article to delve into the financial details of this renowned farm.
With a newfound understanding of their business ventures, I returned to my problem set, armed with a fresh perspective and a satisfying dose of financial knowledge.
4. Check Your Solution
After solving the problem, check your answer to ensure it makes sense and satisfies the given conditions. Consider alternative solutions or approaches to verify your result.
5. Interpret the Solution
Once you have a solution, interpret its meaning and implications. Explain how the solution relates to the original problem and discuss any limitations or assumptions made during the problem-solving process.
Common Errors and Pitfalls
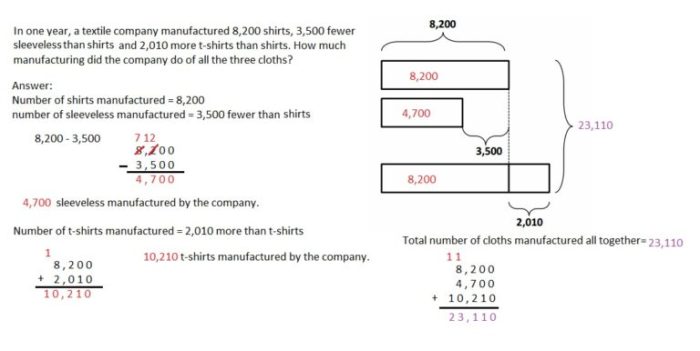
Solving these problems can be challenging, and it’s easy to make mistakes. Let’s explore some common errors and pitfalls to watch out for:
Misunderstanding the Problem
Before attempting to solve a problem, it’s crucial to ensure you understand what it’s asking. Carefully read the problem statement, identify the given information, and determine what you need to find.
Incorrect Assumptions
Don’t assume anything that isn’t explicitly stated in the problem. Making assumptions can lead to incorrect solutions.
Arithmetic Errors
Be careful when performing calculations. Double-check your work to avoid errors in addition, subtraction, multiplication, and division.
Sign Errors
Pay attention to the signs of numbers. A mistake in sign can significantly alter the solution.
Unit Errors
Ensure that your answers are in the correct units. For example, if the problem asks for a length in meters, don’t give the answer in centimeters.
Not Considering All Possibilities
Some problems may have multiple solutions or require you to consider different scenarios. Don’t limit yourself to a single approach; explore all possibilities.
Applications and Extensions
The concepts and methods learned in this problem set have a wide range of real-world applications in various fields.
For instance, the idea of limits can be used to determine the behavior of functions as their inputs approach certain values. This is useful in fields such as physics, where it can be used to describe the motion of objects, or in economics, where it can be used to analyze the behavior of markets.
Extensions and Variations
To foster a deeper understanding of the concepts covered in this problem set, consider the following extensions and variations of the problems:
- Explore the concept of limits using different types of functions, such as rational functions, trigonometric functions, or exponential functions.
- Investigate the relationship between the limit of a function and the continuity of the function.
- Apply the concept of limits to solve real-world problems, such as finding the velocity of an object or the area under a curve.
Learning Objectives and Assessment
This problem set aims to reinforce students’ understanding of key concepts and methods covered in Lesson 19.
Upon completing this problem set, students should be able to:
- Demonstrate proficiency in solving problems involving linear equations.
- Apply algebraic techniques to solve real-world problems.
- Analyze and interpret the solutions obtained from linear equations.
Assessment
Student progress and understanding can be assessed through:
- Problem-Solving Accuracy:Evaluating the correctness and completeness of student solutions.
- Explanation and Reasoning:Assessing students’ ability to provide clear and logical explanations for their solutions.
- Real-World Application:Evaluating students’ ability to apply linear equations to solve practical problems.
General Inquiries
What is the purpose of Lesson 19 Problem Set 7.1?
This problem set aims to enhance your understanding of fundamental mathematical concepts and methods, fostering your ability to solve complex problems and apply mathematical principles to real-world situations.
What are some common errors to avoid in this problem set?
Pay close attention to potential pitfalls such as misinterpreting problem statements, making careless arithmetic errors, and neglecting to justify your reasoning clearly.
How will my progress be assessed in this problem set?
Your progress will be evaluated based on your ability to solve problems accurately, demonstrate logical reasoning, and effectively communicate your solutions.